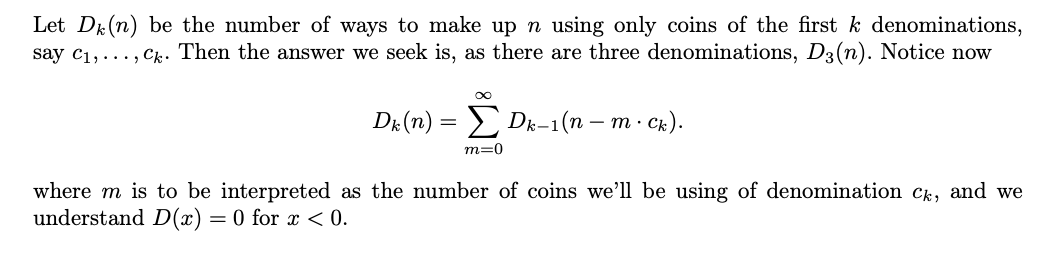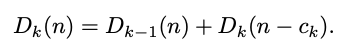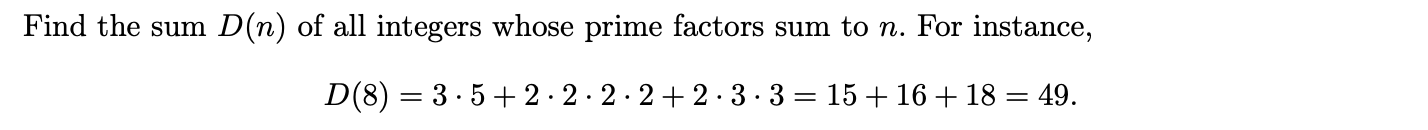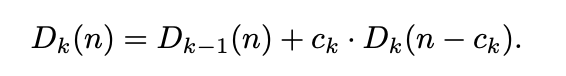‘Coin-change’ recursion

Today, while solving a Project Euler problem, I was made aware of a simple and general trick to simplifying certain recursion problems. For a person with a blog post on recursive problems it is perhaps embarrassing for me to only just now be finding out about this; thus I’ve decided to devote a short sequel post on exploring the so-called ‘coin-change’ trick.

To begin, consider the following problem:

The namesake ‘coin-change’ problem.

For our purposes we aren’t looking for a closed form solution; it suffices to write a program that solves the problem for a given n. What follows is the approach I would’ve used prior to finding out about the coin-change trick:

Yesterday’s naiveté

Compare this to:

Today’s wisdom

Indeed, the second term cleverly takes care of all situations where at least one ‘new’ coin is used. Notice a novel feature here is that it is important to compute the values on each ‘level’ of D in increasing order of n.

The coin-change trick isn’t just useful for counting. Indeed, consider the strongly related Project Euler #618:

The analogy to coin-change is hopefully clear; it should also be clear that in this case